Convolutional Approximations to the General Non-Line-of-Sight Imaging Operator

Byeongjoo Ahn, Akshat Dave, Ashok Veeraraghavan, Ioannis Gkioulekas, and Aswin C. Sankaranarayanan

Abstract

Non-line-of-sight (NLOS) imaging aims to reconstruct scenes outside the field of view of an imaging system. A common approach is to measure the so-called light transients, which facilitates reconstructions through ellipsoidal tomography that involves solving a linear least-squares. Unfortunately, the corresponding linear operator is very high-dimensional and lacks structures that facilitate fast solvers, and so, the ensuing optimization is a computationally daunting task. We introduce a computationally tractable framework for solving the ellipsoidal tomography problem. Our main observation is that the Gram of the ellipsoidal tomography operator is convolutional, either exactly under certain idealized imaging conditions, or approximately in practice. This, in turn, allows us to obtain the ellipsoidal tomography solution by using efficient deconvolution procedures to solve a linear least-squares problem involving the Gram operator. The computational tractability of our approach also facilitates the use of various regularizers during the deconvolution procedure. We demonstrate the advantages of our framework in a variety of simulated and real experiments.

Key Idea

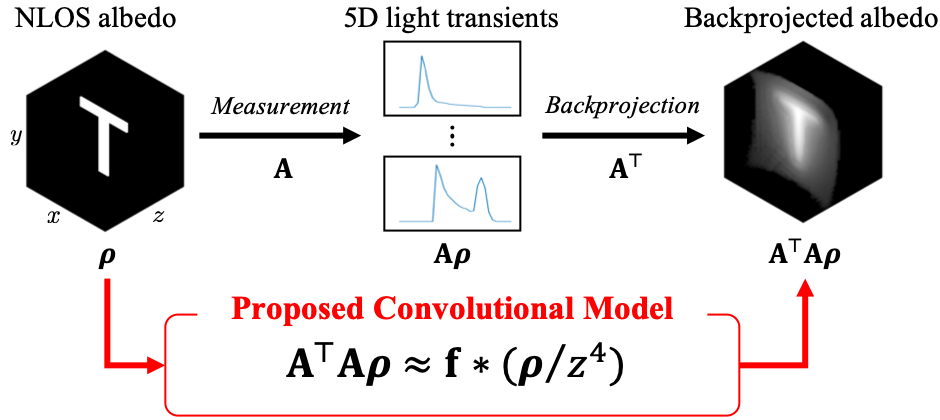
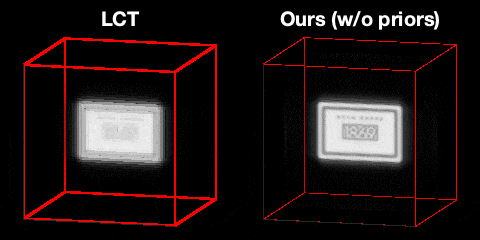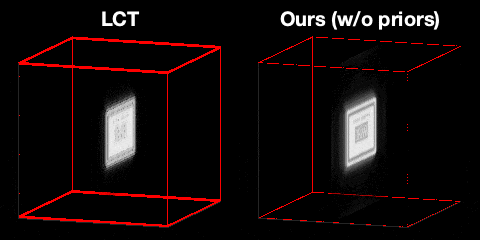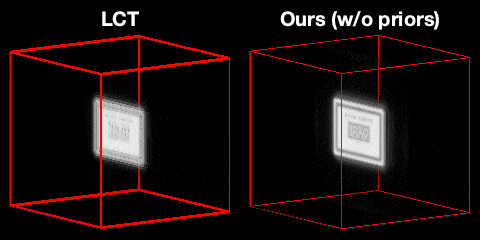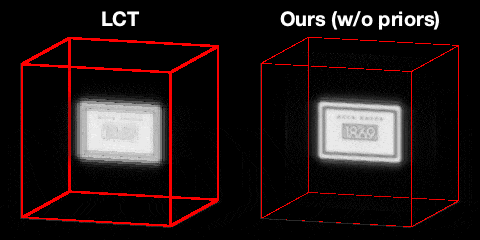
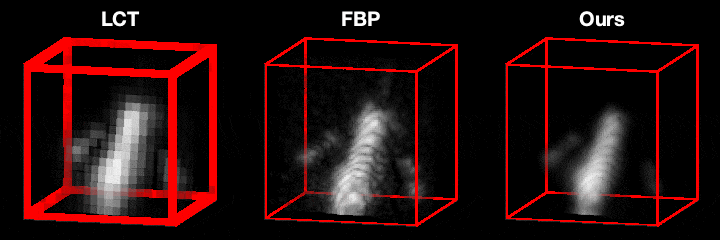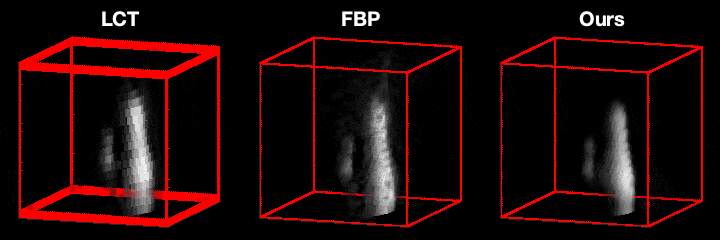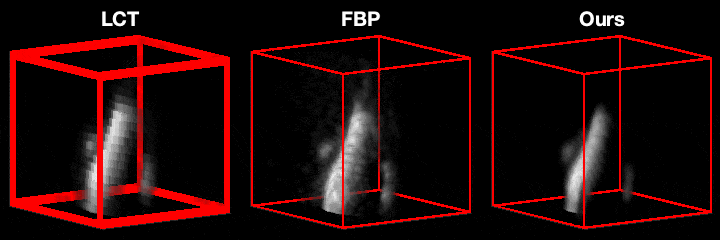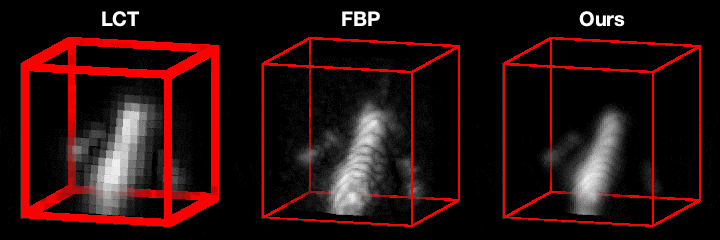
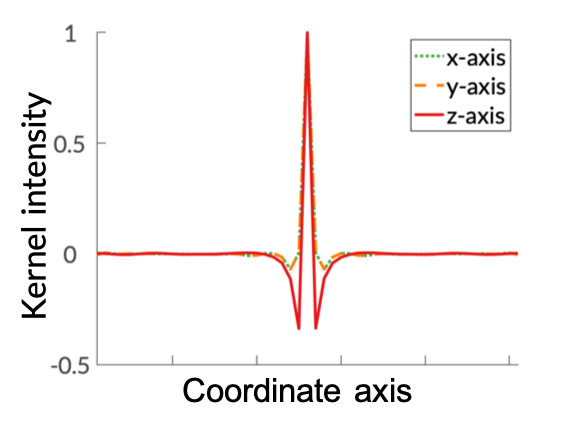
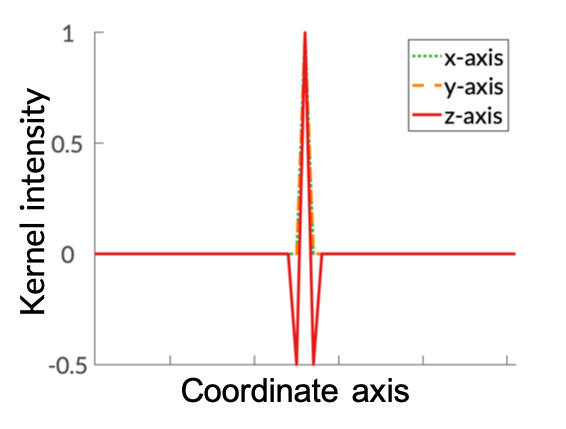
Our main technical result is to show that, under certain assumptions on the imaging geometry, the Gram of the NLOS measurement operator is a convolution operator. This result advances NLOS imaging in three important ways. First, it allows us to efficiently obtain the ellipsoidal tomography reconstruction by solving an equivalent linear least-squares involving the Gram operator: As the Gram operator is convolutional, this problem can be solved using computationally-efficient deconvolution algorithms. Second, it provides a theoretical justification for the filtered backprojection algorithm: We can show that filtered backprojection corresponds to using an approximate deconvolution filter to solve the problem involving the Gram operator. Third, it facilitates the use of a wide range of priors to regularize the NLOS reconstruction problem: The convolutional property of the Gram operator implies that the corresponding regularized least squares remain computationally tractable.

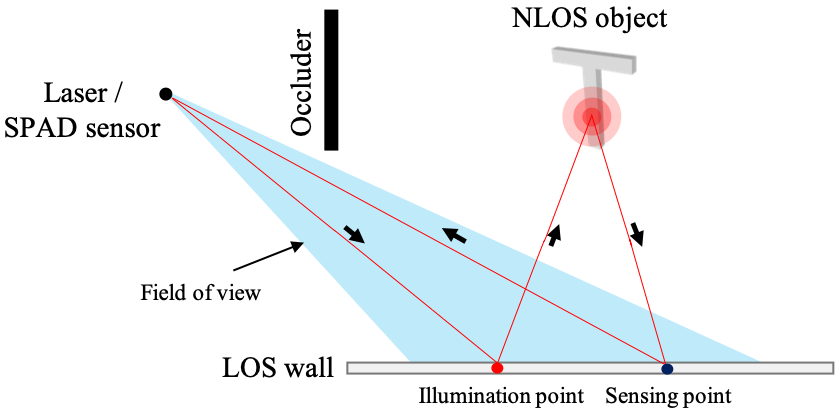
NLOS imaging setup

Convolutional approximations

Experiments

We compare our algorithm against full linear reconstruction, filtered backprojection (FBP), and light cone transform (LCT), on simulated and real transients. Note that the thicker red lines in LCT indicates a lower resolution of the result caused by the inherent limit of the method.

Simulated results

Comparisons with full linear reconstruction

Our method has faster runtime, while providing similar reconstruction quality.


Comparisons with filtered backprojection

Even without the use of priors, our method performs better, as it uses the exact inverse filter whereas filtered backprojection behaves as a heuristic inverse filter.


Comparisons with light cone transform

Even though the temporal resolution of the light transient is enough to reconstruct the letters on the soap, it is not reconstructed well in LCT due to the poor lateral resolution. On the other hand, we can recover significantly higher detail by running the same confocal measurements through our computational pipeline even without any prior.

Real scenes

We observe that our method provides higher reconstruction detail than LCT, by exploiting the high temporal resolution of transients, and fewer artifacts than filtered backprojection, by incorporating accurate inverse kernels and priors. We used a mixed prior that enforces positivity, total variation, as well as canonical sparsity.


Inverse Kernel

We observe that the inverse kernel closely resembles a Laplacian filter. This similarity lends theoretical support to the common choice of the Laplacian filter for post-processing in filtered backprojection. However, we must highlight two important differences. First, the discrete Laplacian filter is bereft of spatial scale. As a consequence, the result of traditional filtered backprojection is expected to change when we voxelize the NLOS scene at different resolutions. Our derived kernel and its inverse have no such adverse properties. Second, the inverse kernel in the figure was derived under the two assumptions required for our proposition of the convolutional Gram operator. When these assumptions do not hold, we can use eigendecomposition as discussed above to derive an approximate inverse kernel that can be significantly different from the Laplacian filter. Unlike filtered backprojection, our approach naturally accommodates for this by using the correct inverse filter.

Inverse kernel (ours) - 1D slice

Laplacian kernel - 1D slice

More Details

For an in-depth description of the technology behind this work, please refer to our paper and supplemental material.

Byeongjoo Ahn, Akshat Dave, Ashok Veeraraghavan, Ioannis Gkioulekas, Aswin C. Sankaranarayanan, "Convolutional Approximations to the General Non-Line-of-Sight Imaging Operator", ICCV 2019
Link to paper

Paper
Link to supplemental material

Supplemental material
Link to poster

Poster

Code

Our implementation is available at the following GitHub repository.

Link to paper

Acknowledgements

We thank Kiriakos Kutulakos and Srinivasa Narasimhan for helpful discussions. This work was supported by DARPA REVEAL (HR0011-16-C-0025, HR0011-16-C-0028) and NSF Expeditions (CCF-1730574, CCF-1730147) grants. B. Ahn is supported by the Korea Foundation for Advanced Studies.

Copyright © 2019 Byeongjoo Ahn