A Theory of Fermat Paths for Non-Line-of-Sight Shape Reconstruction

Shumian Xin, Sotiris Nousias, Kiriakos N. Kutulakos, Aswin C. Sankaranarayanan, Srinivasa G. Narasimhan, and Ioannis Gkioulekas

Abstract

We present a novel theory of Fermat paths of light between a known visible scene and an unknown object not in the line of sight of a transient camera. These light paths either obey specular reflection or are reflected by the object’s boundary, and hence encode the shape of the hidden object. We prove that Fermat paths correspond to discontinuities in the transient measurements. We then derive a novel constraint that relates the spatial derivatives of the path lengths at these discontinuities to the surface normal. Based on this theory, we present an algorithm, called Fermat Flow, to estimate the shape of the non-line-of-sight object. Our method allows, for the first time, accurate shape recovery of complex objects, ranging from diffuse to specular, that are hidden around the corner as well as hidden behind a diffuser. Finally, our approach is agnostic to the particular technology used for transient imaging. As such, we demonstrate mm-scale shape recovery from pico-second scale transients using a SPAD and ultrafast laser, as well as micron-scale reconstruction from femto-second scale transients using interferometry. We believe our work is a significant advance over the state-of-the-art in non-line-of-sight imaging.

Non-Line-of-Sight Imaging

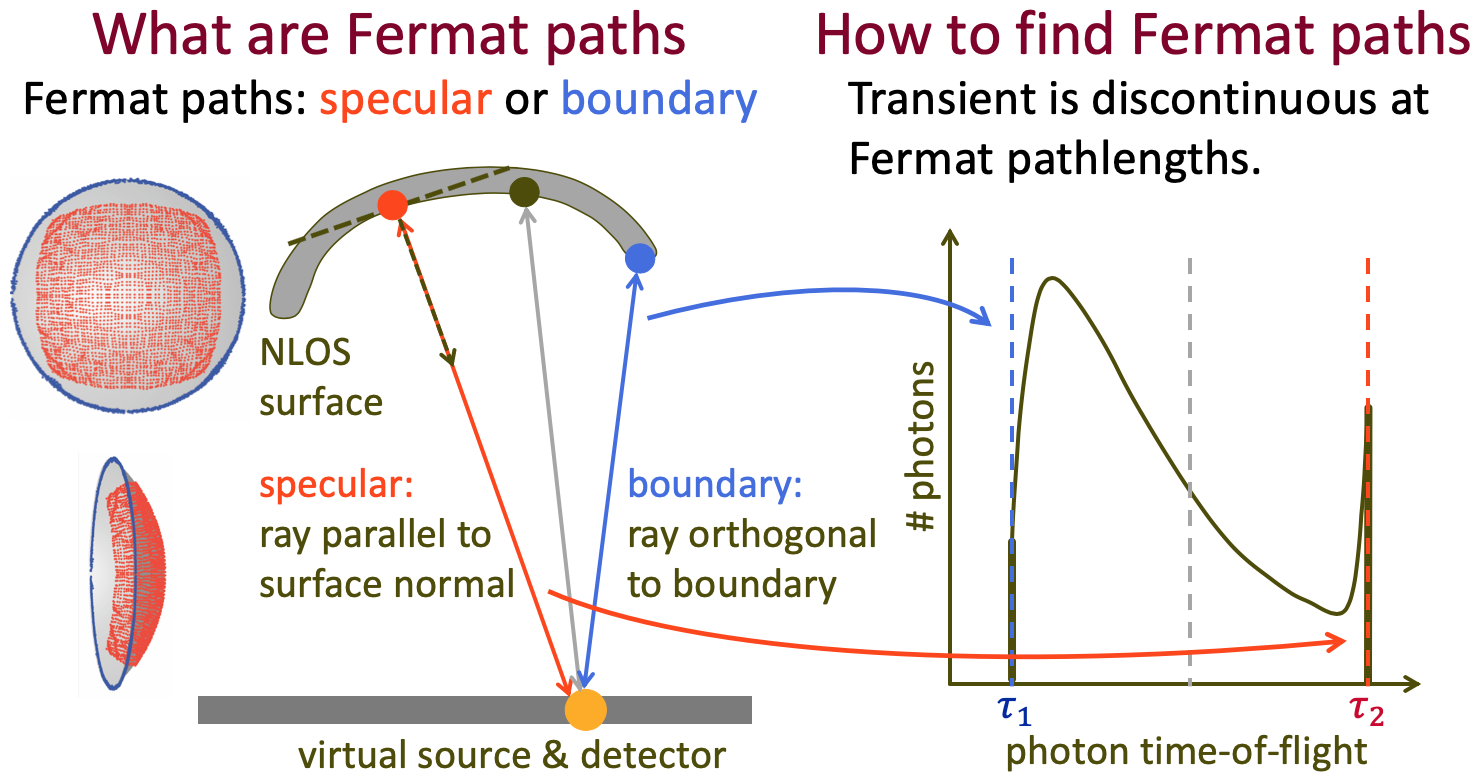
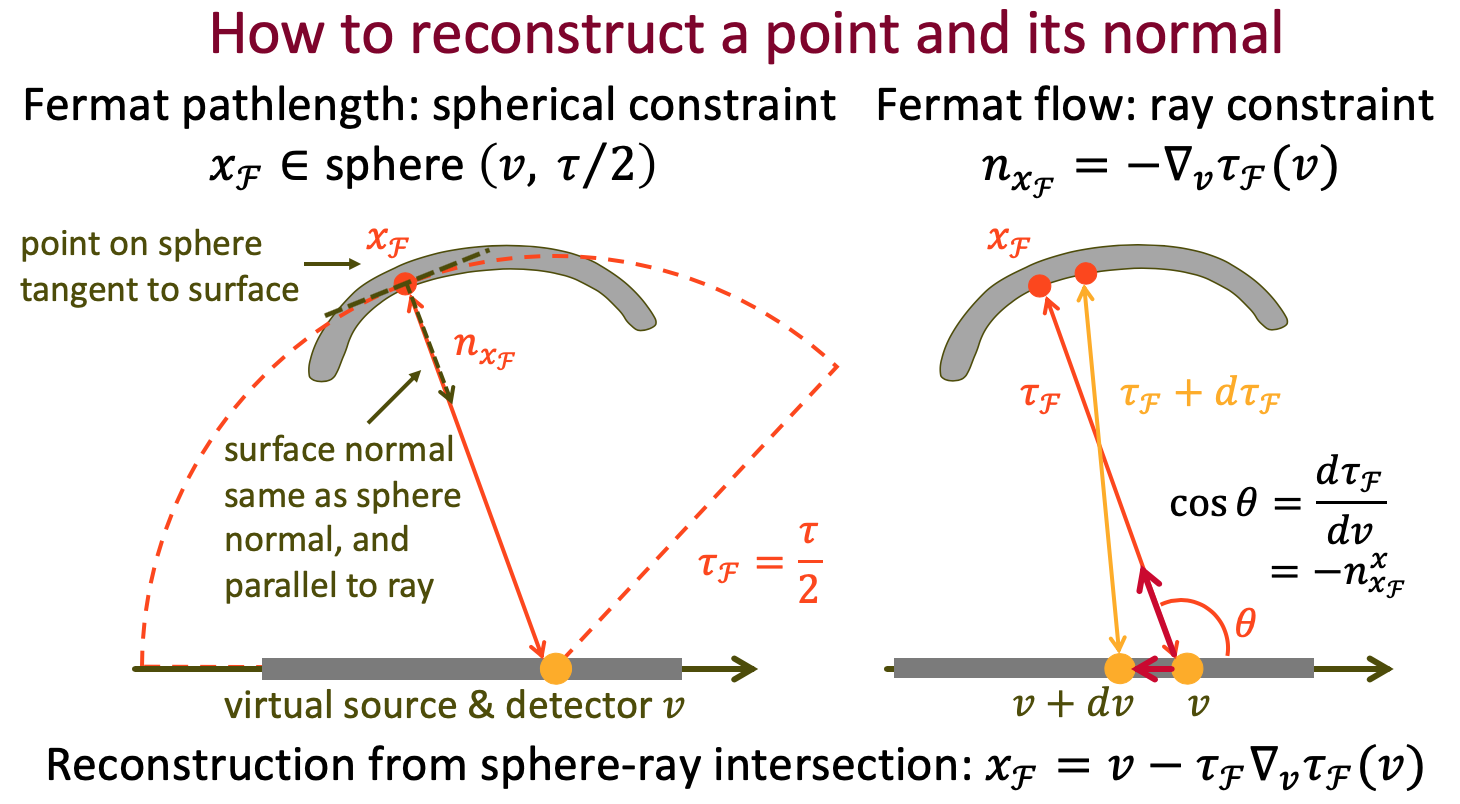
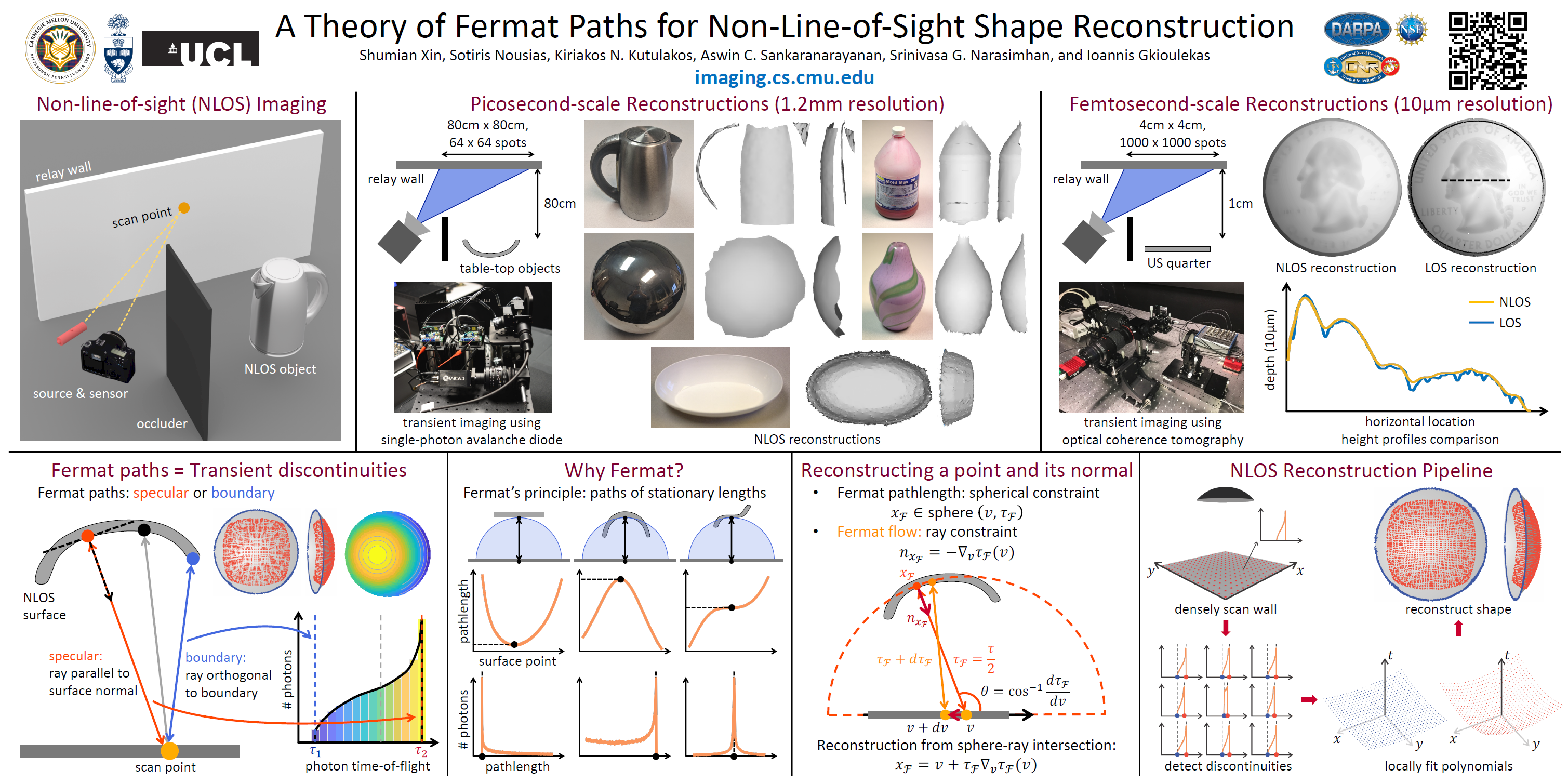
When talking about Non-Line-of-Sight (NLOS) imaging, we mainly refer to two scenarios. The first scenario consists of an active light source and a sensor, which are collocated, and are looking at some diffuse surfaces, e.g. a wall. The scene also contains an object that is outside the field-of-view of the sensor. We then use the measurements captured by the sensor to reconstruct this object. We refer to this senario as "looing around the corner".

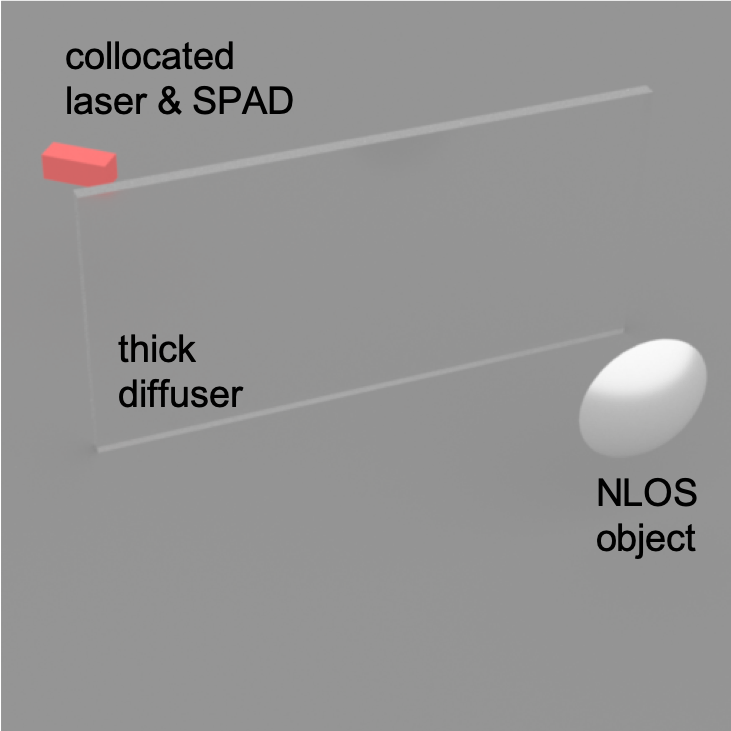
Alternatively, in the second scenerio, the object maybe within the field-of-view of the sensor, but are occuluded by some thick diffuser, e.g. a piece of paper. We refer to this scenario as "looking through a diffuser".

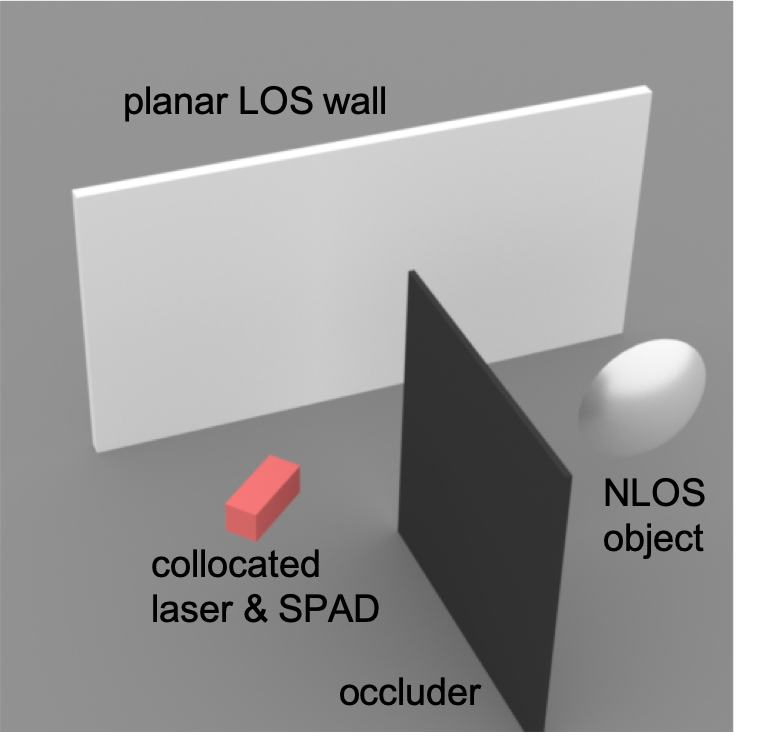
looking around the corner

looking through a diffuser

Experiments

All experiments are based on measurements captured with two transient imaging setups, one operating at picosecond and the other at femtosecond temporal scales.

Picosecond-scale Experiments

Imaging System

We use a SPAD-based transient imaging system consisting of a picosecond laser (NKT SuperK EXW-12), a SPAD detector (MPD module), and a time-correlated single photon counter (TCSPC, Pico-Quant PicoHarp). The temporal binning resolution of the TCSPC unit is 4 ps, for an absolute upper bound in depth resolution of 1.2mm. We use galvo mirrors to independently control viewpoint and illumination direction, and perform both confocal and non-confocal scanning in the looking-around-the-corner setting.

Reconstructions

We scanned a variety of every day objects, with convex and concave geometry of different BRDFs, including translucent (plastic jug), glossy (bowl, vase), rough specular (kettle) and smooth specular (sphere). Most of the objects have a major dimension of approximately 20 - 30cm, and are placed at a distance of 80 cm from the visible wall. We use confocal scanningwith a grid of 64 * 64 points distributed in an area of 80cm * 80cm on the visible wall.

Femtosecond-scale Experiments

Imaging System

We use a time-domain, full-frame optical coherent tomography system. We use this system to perform confocal scans under both the looking-around-the-corner and looking-through-diffuser settings. We use spatially and temporally incoherent LED illumination, which allows us to combine transient imaging with diagonal probing. In the context of confocal scanning, this means that we can simultaneously collect transients at all points on the visible surface without scanning, as transient measurements taken at one point will not be contaminated with light emanating from a different point. Our implementation has depth resolution of 10um.

Coin Reconstructions

We perform experiments in both the looking-around-the-corner and looking-through-diffuser settings, where for the diffuser we use a thin sheet of paper. In both cases, the NLOS object is a US quarter, with the obverse side facing the visible surface. We place the coin at a distance of 10mm from the visible surface, and collect transient measurements on an area of about 40mm * 40mm, at an 1 MPixel grid of points. For validation, we additionally use the same setup to directly scan the coin without occlusion.

What are Fermat Paths?

Fermat paths are the paths that satisfy Fermat's principle, meaning they have locally stationary pathlengths. Fermat paths are either specular paths or at object boundary. They are purely geometric, and are invariant to BRDF. In this work, we use Fermat paths for shape reconstruction.

For more details, please refer to the video below.

Fermat Flow Constraint

After detecting Fermat paths and their corresponding pathlengths, what can we tell about the points corresponding to these paths?

First, the point must be on a sphere with the collocated virtual source and detector as its center, and half the Fermat pathlength as its radius. Next, we derive the ray constraint which we call the "Fermat flow" constraint. Then, we conduct sphere-ray intersection to pin down the point.

For more details, please refer to the video below.

More Details

For an in-depth description of the technology behind this work, please refer to our paper, supplementary material, CVPR poster, CVPR talk slides, and the accompanying video.

Shumian Xin, Sotiris Nousias, Kiriakos N. Kutulakos, Aswin C. Sankaranarayanan, Srinivasa G. Narasimhan, and Ioannis Gkioulekas. "A Theory of Fermat Paths for Non-Line-of-Sight Shape Reconstruction", CVPR 2019

Link to paper

Sponsors

This work was supported by the DARPA REVEAL program under contract HR0011-16-C-0025. SX, ACS, SGN, and IG were additionally supported by NSF Expeditions award CCF-1730147. KNK was supported by the NSERC RGPIN and RTI programs. Some equipment was supported by ONR DURIP award N00014-16-1-2906.

Copyright © 2019 Shumian Xin