Towards Learning-based Inverse Subsurface Scattering

Given images of translucent objects, of unknown shape and lighting, we aim to use learning to infer the optical parameters controlling subsurface scattering of light inside the objects. We introduce a new architecture, the inverse transport network (ITN), that aims to improve generalization of an encoder network to unseen scenes, by connecting it with a physically-accurate, differentiable Monte Carlo renderer capable of estimating image derivatives with respect to scattering material parameters. During training, this combination forces the encoder network to predict parameters that not only match groundtruth values, but also reproduce input images. During testing, the encoder network is used alone, without the renderer, to predict material parameters from a single input image. Drawing insights from the physics of radiative transfer, we additionally use material parameterizations that help reduce estimation errors due to ambiguities in the scattering parameter space. Finally, we augment the training loss with pixelwise weight maps that emphasize the parts of the image most informative about the underlying scattering parameters. We demonstrate that this combination allows neural networks to generalize to scenes with completely unseen geometries and illuminations better than traditional networks, with 38.06% reduced parameter error on average.

The common cause of the characteristic appearance of translucent materials is sub-surface scattering: As photons reach the surface of a translucent object, they continue traveling in its interior, where they scatter, potentially multiple times, before reemerging outside the object. Broadly speaking, we can break sub-surface scattering problems down into two categories. The first category is forward scattering problems, which attempt to predict the appearance of a translucent object, assuming that the optical parameters control- ling scattering of light at its interior are known. The second category, and the focus of this paper, is inverse scattering problems: Given images of a translucent object, they attempt to predict its underlying scattering parameters.

Among existing approaches for inverse scattering, many are based on simplifying assumptions about volume light transport, such as single scattering (all photons scatter once) and diffusion (all photons scatter a very large number of times). These assumptions limit the applicability of these methods to very optically-thin and thick materials. Alternatively, recent years have seen the development of general-purpose inverse scattering techniques, which combine analysis by synthesis and Monte Carlo volume rendering in order to accurately estimate material parameters without the need for simplifications. Despite their broad applicability, these techniques can be prohibitively computationally expensive: processing measurements of a new material often requires performing hundreds of expensive Monte Carlo rendering operations.

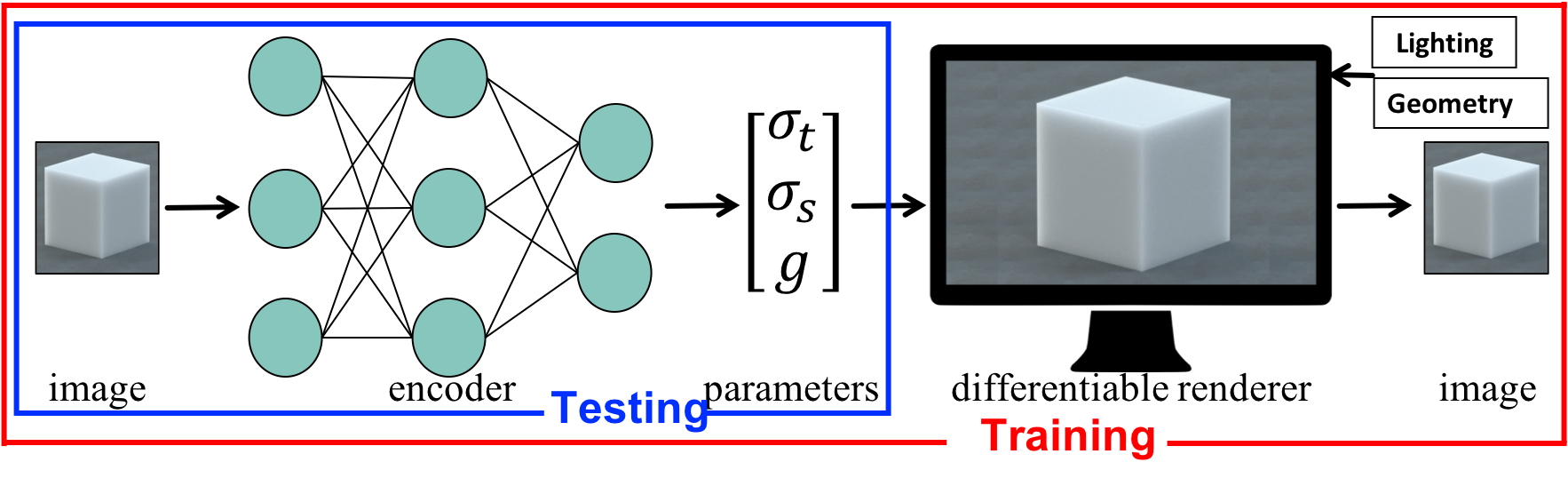
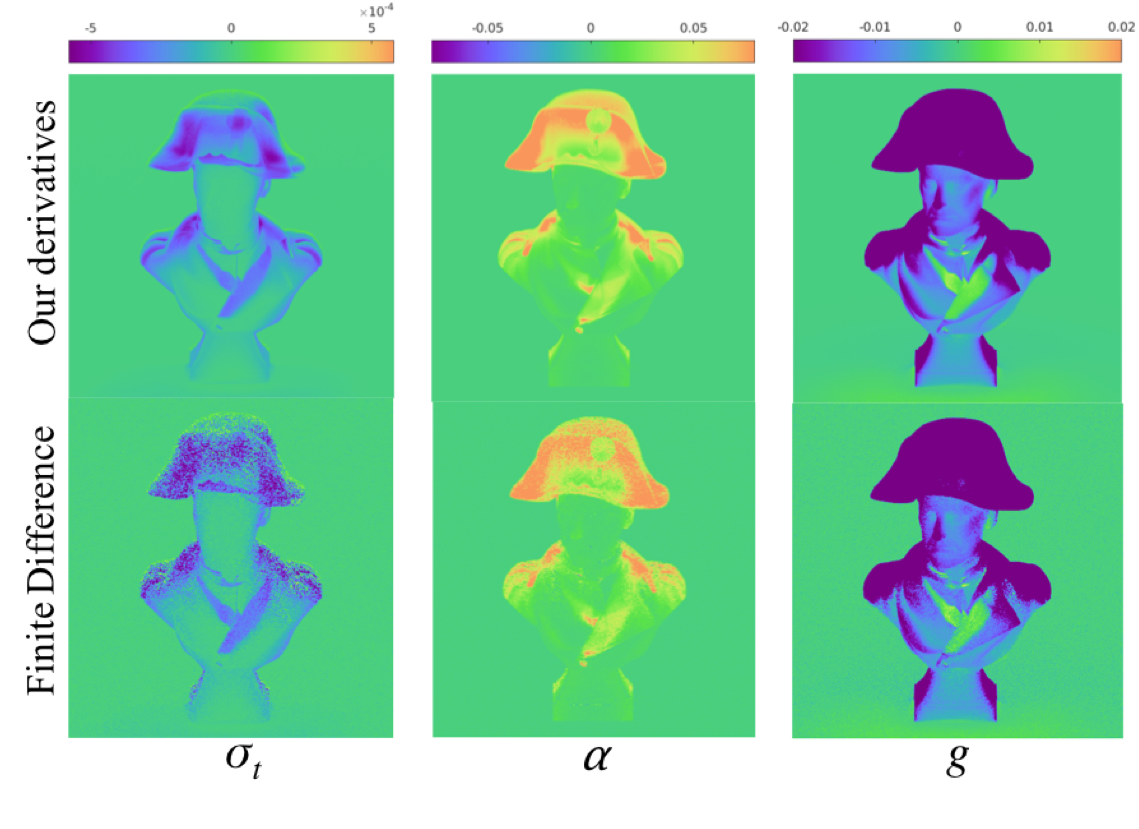
We propose a physics-aware learning pipeline that we term inverse transport networks (ITN), which aims to combine the computational efficiency of learning-based approaches with the generality of analysis by synthesis approaches for inverse scattering. We further tailor these neural networks towards inverse scattering, by taking into account results from the radiative transfer literature, characterizing the conditions under which different scattering materials can produce similar translucent appearance. We introduce ways for making our networks robust to these ambiguities, including the use of nonlinear material parameterizations, and weight maps emphasizing pixels where these ambiguities are weaker.

We use our own implementation of differentiable rendering: We integrated the Stan Math Library for automatic differentiation of throughput terms, with the Mitsuba engine for physically accurate Monte Carlo rendering. Even though our focus is on inverse scattering, our implementation is a general-purpose differentiable renderer that can compute derivatives for scene parameters such as normals, reflectance, and illumination. We verified correctness of our derivatives by comparing derivatives computed using finite differences.

For our quantitative comparisons, we use a synthetic dataset containing images of translucent objects with varying geometry, illumination, and material parameters. We use ten different object shapes, selected to have a variety of thin and thick geometric features, each placed under ten different illumination conditions created using the Hosek-Wilkiesun-sky model. For each shape and illumination combination, we render images for different parameters π that include σt ∈ [25 mm−1 , 300 mm−1], α ∈ [0.3,0.95], and Henyey-Greenstein phase functions fp with parameter g ∈ [0, 0.9]. We use the Mitsuba physics-based renderer to simulate 30,000 high-dynamic range images under these settings.

We use each network to predict material parameters, and evaluate the predictions using three metrics: 

1. A parameter loss comparing it to the groundtruth parameters. 
2. An appearance loss comparing the reconstructed and input images.
3. An appearance loss between renderings for a novel scene.

To summerize the results, the ITN with similarity-aware parameterization and weight maps outperforms the other networks in most metrics. Our networks can produce material parameter estimates that are on average 38.06% more accurate than those produced by baseline regression networks. Furthermore, images rendered with our predictions are on average 53.82% closer to the groundtruth. Some visual comparisons among images rendered with predicted parameters are shown below.