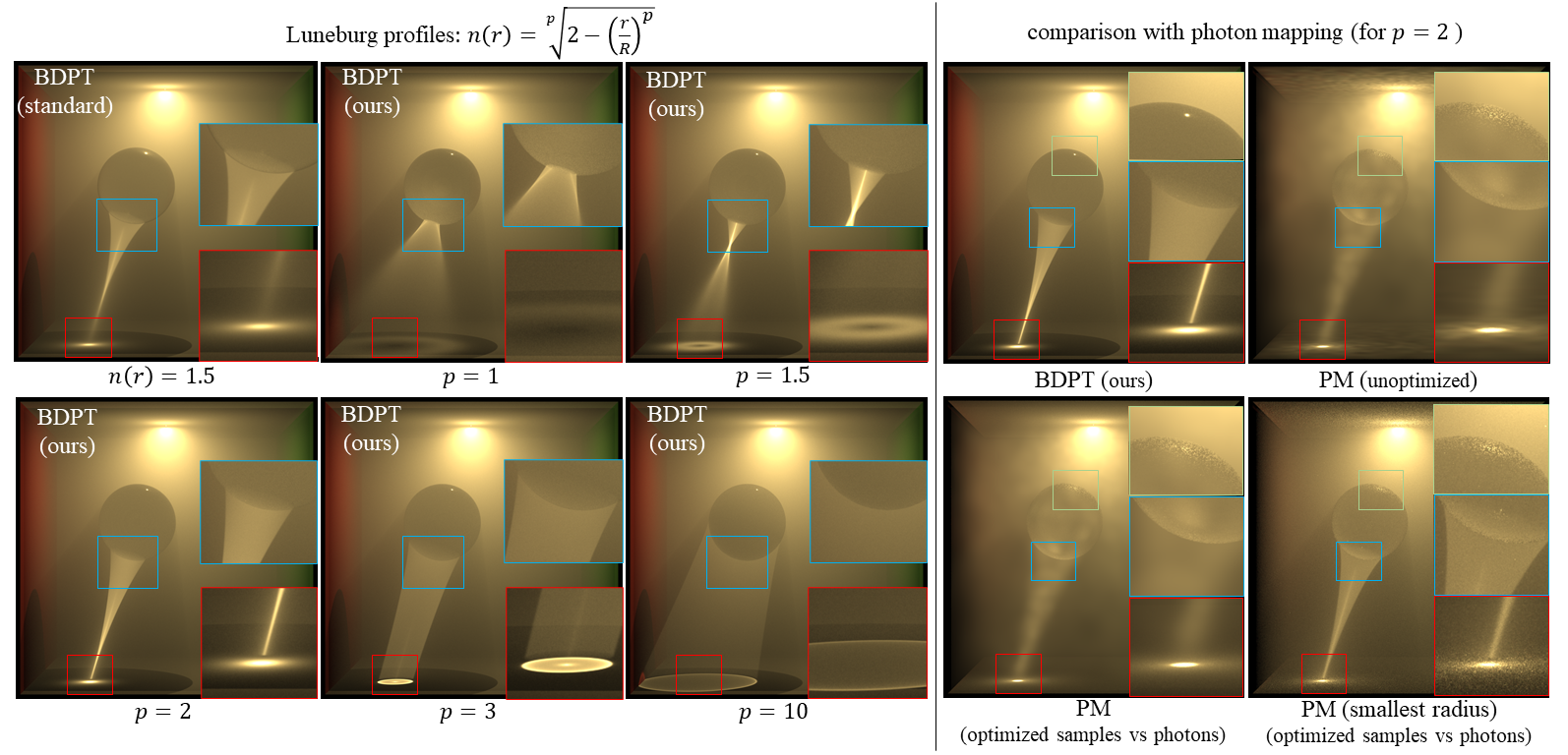
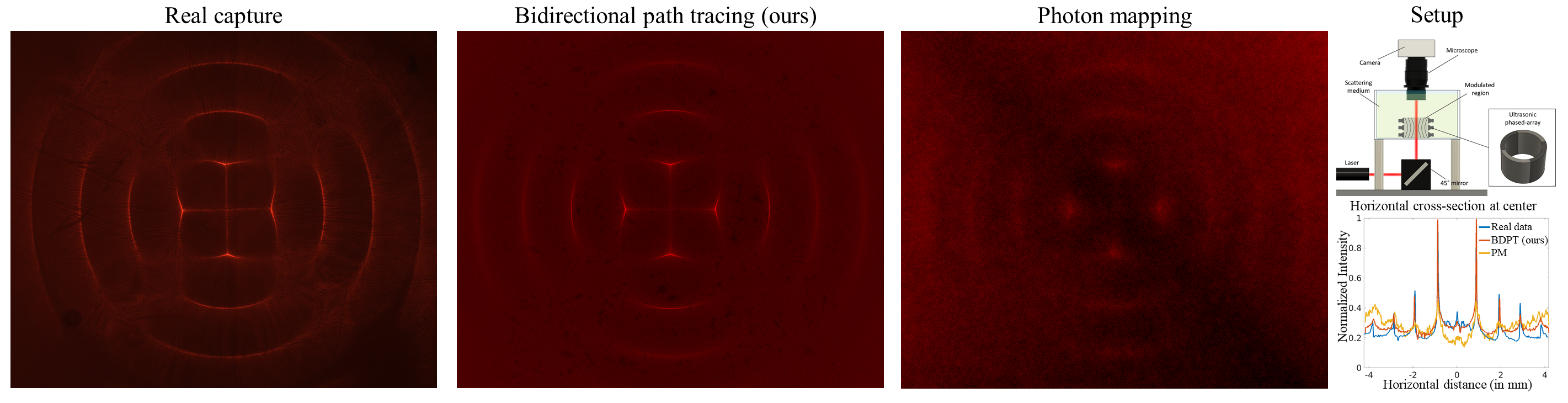
Heterogeneous refractive media
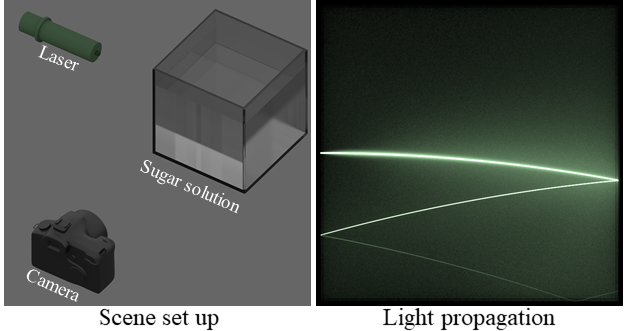
Media characterized by continuously-varying refractive index, occurring due to variations in temperature and pressure, or due to heterogeneous mixing of materials, are common in the real world. Examples of such heterogeneous refractive media include the atmosphere, biological tissue, crystals, minerals, and transparent plastics. When light travels through such media, it follows curved trajectories due to the continuous refraction. This bending of light can be observed by shining a laser beam on a heterogeneous refractive medium, e.g., as shown in figure to the right.
The aquarium shown to the left of the figure is filled with a sugar solution whose refractive index increases linearly with the liquid's depth. A laser beam propagating through this solution refracts and scatters continuously, resulting in a curved light trajectory. Multiple such trajectories appear due to Fresnel reflection of the beam on the aquarium's wall.