Solving partial differential equations in participating media

Bailey Miller, Rohan Sawhney, Keenan Crane, Ioannis Gkioulekas

ACM Transactions on Graphics (SIGGRAPH) 2025

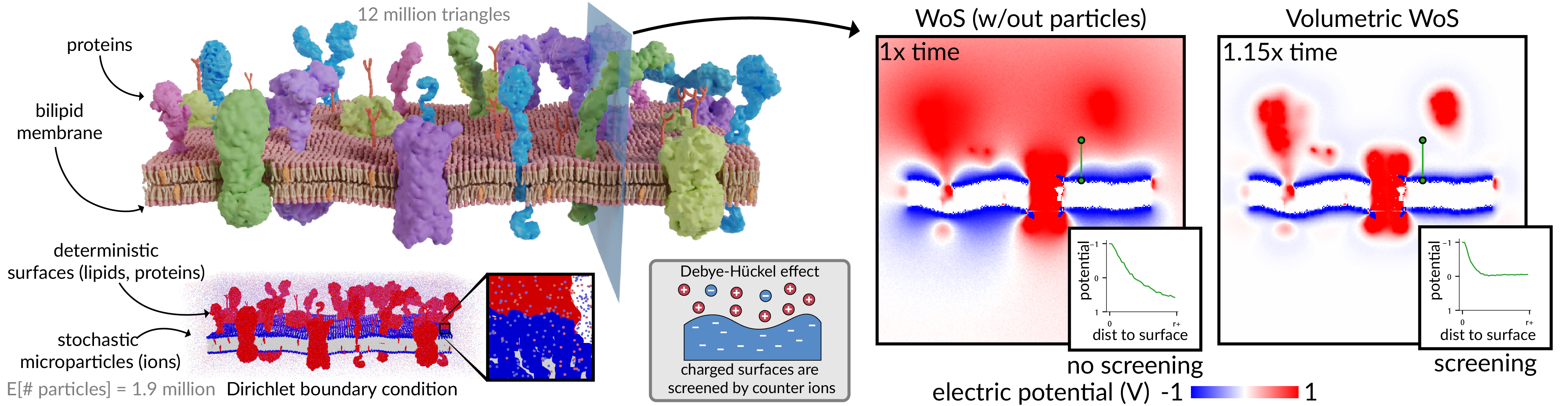
teaser
Real physical systems, such as biomembranes, have extraordinarily complex geometry, often managed by homogenizing particulate substances that mediate physical interactions. For example, in the setup we show, a homogenized PDE is commonly used to model electrostatic screening due to ions in solution. In reality, however, homogenization can be highly inaccurate, as particles often exhibit a scale similar to geometric features. We develop Monte Carlo methods that directly account for both particle and boundary geometry, maintaining efficiency without any limiting assumptions or geometric simplification.

Abstract

We consider the problem of solving partial differential equations (PDEs) in domains with complex microparticle geometry that is impractical, or intractable, to model explicitly. Drawing inspiration from volume rendering, we propose tackling this problem by treating the domain as a participating medium that models microparticle geometry stochastically, through aggregate statistical properties (e.g., particle density). We first introduce the problem setting of PDE simulation in participating media. We then specialize to exponential media and describe the properties that make them an attractive model of microparticle geometry for PDE simulation problems. We use these properties to develop two new algorithms, volumetric walk on spheres and volumetric walk on stars, that generalize previous Monte Carlo algorithms to enable efficient and discretization-free simulation of linear elliptic PDEs (e.g., Laplace) in participating media. We demonstrate experimentally that our algorithms can solve Laplace boundary value problems with complex microparticle geometry more accurately and more efficiently than previous approaches, such as ensemble averaging and homogenization.

Resources

Paper: Our paper is available here.

Code: Our code will be available soon.

Citation

@article{Miller:VWoS:2025,
	author = {Miller, Bailey and Sawhney, Rohan and Crane, Keenan and Gkioulekas, Ioannis},
	title = {Solving partial differential equations in participating media},
	year = {2025},
	issue_date = {July 2025},
	publisher = {Association for Computing Machinery},
	address = {New York, NY, USA},
	volume = {44},
	number = {4},
	issn = {0730-0301},
	url = {https://doi.org/10.1145/3731152},
	doi = {10.1145/3731152},
	journal = {ACM Trans. Graph.},
	month = {jul},
	numpages = {20}
}

Acknowledgments

This work was supported by National Science Foundation (NSF) award 2212290; National Institute of Food and Agriculture award 2023-67021-39073; a gift from nTopology; NSF Graduate Research Fellowship DGE2140739 and an NVIDIA graduate fellowship for Bailey Miller; a Packard Foundation Fellowship for Keenan Crane; and Alfred P. Sloan Research Fellowship FG202013153 for Ioannis Gkioulekas. Rohan Sawhney thanks Ken Museth for supporting this work. The protein model (Figure 1) is from user QuadroFlow on TurboSquid. The ginseng root model (Figures 9(d–f), 12(b)) is from user 3dror on TurboSquid. The mushroom model (Figures 9(a–c), 12(a)) and the connector model (Figures 10, 12(c)) are from the Thingi10k dataset [Zhou and Jacobson 2016]. The cloud model (Figure 13) is from the pbrt-v3 scene repository [Pharr et al. 2018].