Simulated Noisy Scenes - Comparison
Using a rotating PSF is much more light efficient, and robust to noise than past approaches based on spatial-multiplexing optics. In short, while other approaches rely on capturing just a subset of the available light, our system captures all of the available light because the entire sensor is always exposed. In addition, because the signal from different times is intermixed together on the sensor, the effect of read noise is minimized. This makes our approach effective in low-light scenarios, as shown by the below simulated examples
For the scenes on this webpage, we simulated the resultant images from a scene where the intensity of the brightest scene point was set to some f of the saturation point of the sensor. The energy of this point is then distributed over the sensor by its point-spread function.
The word "test" moves in a sinusoidal pattern across the scene.
f = 0.03125
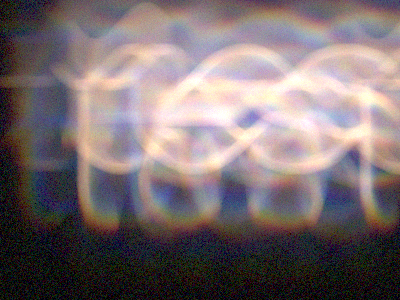


Observe that our method (first row right) reconstructs the moving "test" significantly better than prior work under noisy conditions.
The word "iccv" moves in a sinusoidal pattern across the scene.
f = 0.03125



Again, our method (first row right) recovers this scene with more intensity variation much better than prior work.
A point varies in intensity over time.
f = 8



Our method (first row right) can resolve the fast flickering of a simulated LED, while past methods fail due to their poor light efficiency.